In the spirit of the holiday season, this is a series of short blog posts covering random things I have learned while doing Salesforce development, one for each day of Advent.

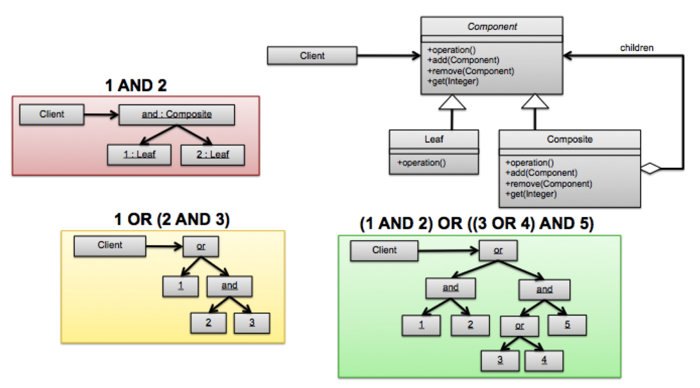
On the 13th advent day we started to talk about building a rules engine in Apex. Before we get into that implementation, a key part of it was using the Composite design pattern to evaluate a logical expression. In summary, the composite pattern is used to represent a group of objects that are treated the same way as a single instance of the same type of object.

For example, consider the logical expression 1 AND 2. As a whole, it can be evaluated to true or false. However, the statement is also two separate statements: the statement 1 and the statement 2, both of which can also be evaluated to true or false. Using the composite pattern, we would be able to capture these statments into objects that can evaluate to true or false.

Salesforce actually has a great article on the topic: [https://developer.salesforce.com/page/Apex_Design_Patterns_-Composite](https://developer.salesforce.com/page/Apex_Design_Patterns-_Composite)

They even use the example of capturing workflow rule logic! When I found this I thought I didn’t have to write anything new after all and I could just use this code. But later down I read the following:

Note: This article will not cover developing the actual screen or parsing the expression - this article is limited to representing an expression in Apex.

Alright fine, make me do work. Unfortunately the parsing of the expression was what I was really worried about, but at least this gets us half way there in evaluating the parsed expression. Let’s walk through their code sample:

First, there is the Expression interface.

public interface Expression {
    Expression add(Expression expr);
    Expression set(String name, Boolean value);
    Boolean evaluate();
}

Let’s not get too into the details yet, but for now let’s just consider an Expression as something that can be evaluated (i.e. it returns true or false).

In their example, their first implementation of Expression is an abstract class called Composite

public abstract class Composite implements Expression{
    public List<Expression> children {get; private set;} 
    public Composite(){ this.children = new List<Expression>(); }
    public Expression add(Expression expr){
        children.add(expr); return this;
    }
    public Expression set(String name, Boolean value){
        for(Expression expr : children) expr.set(name,value);
        return this;
    }
    public abstract Boolean evaluate();
    public Boolean hasChildren{get{ return !children.isEmpty(); }}
}

You can think of a Composite object as a collection of Expressions, which in this case it captures in the children property. And by evaluating the children objects, the Composite object is itself an Expression that can also be evaluated to true or false.

Let’s look at the extensions of the Composite class to see how this evaluation works:

The AndComposite class has one implemenation of the evaluate method. Basically it iterates over every Expression object in children and if all of them evaluate to true, then it returns true. That fits the description of an “AND” logical statement - all of its parts must evaluate to true in order to be true.

public class AndComposite extends Composite{
    public override Boolean evaluate(){
        for(Expression expr : children) {
            if(!expr.evaluate()) {
              return false;
            }
        }

        return true;
    }
}

The OrComposite class works in a similar fashion, except only ONE of the Expression objects in children needs to evaluate to true. That also fits the description of how an “OR” logical statement works. Only one part of it must evaluate to true in order to be true.

public class OrComposite extends Composite{
    public override Boolean evaluate(){
        for(Expression expr : children) {
            if(expr.evaluate()) {
                return true;
            }
        }
        return false;
    }
}

The last part we need to capture are the most granular logical statements. For example, if 1 AND 2 can be represented by an AndComposite object, we need something to represent the children expressions for the tokens 1 and 2. Here is where the Variable class comes in:

public class Variable implements Expression{
    public String  name  {get;private set;}
    public Boolean value {get;private set;}

    public Variable(String name){ this.name = name; }

    public Expression add(Expression expr){ return this; }

    public Expression set(String name, Boolean value){ 
        if(this.name != null && this.name.equalsIgnoreCase(name)) {
            this.value = value;
        }
        return this; 
    }
    public Boolean evaluate(){ return value; }
}

The Variable object has a name to help us track our it within the Composite as well as value to track its Boolean value. But as you can see, all of these different implementations are Expression objects and as such each of them can evaluate to true or false. We can evaluate a Variable on it’s own or evaluate them together in a Composite. And because Composites evaluate to a single boolean value, they can be combined to create even more complex statements.

For example, let’s say you have the statement (1 AND 2) OR (3 AND 4)

Let’s break this down into it’s parts:

• (1 AND 2) will evaluate into a single Boolean, which we can call A
• (3 AND 4) will evaluate into a single Boolean, which we can call B
• That condenses our statement into a more simple expressions A OR B

You can start to see how breaking it down like this allows you to condense more complex logic.

Now let’s see these classes in action:

First a simple expression: 1 AND 2

Expression expr = new AndComposite();
expr.add(new Variable('1')); //Add a variable with the name `1` to our composite
expr.add(new Variable('2')); //Add a variable with the name `2` to our composite

//the Composite class iterates through all of it's children variables and sets the Boolean value based on its name
expr.set('1', true); 
expr.set('2', false);

System.debug(expr.evaluate()); //false

Now let’s try our more complex statement (1 AND 2) OR (3 AND 4)

//Break down our expression into parts:
Expression exprA = new AndComposite();
expr.add(new Variable('1'));
expr.add(new Variable('2'));

Expression exprB = new AndComposite();
expr.add(new Variable('3'));
expr.add(new Variable('4'));

//Combine those parts
Expression complexExpression = new OrComposite();
complexExpression.add(exprA);
complexExpression.add(exprB);

//The complex composite can still set the children variables directly
complexExpression.set('1', true); 
complexExpression.set('2', false);
complexExpression.set('3', true); 
complexExpression.set('4', true);

System.debug(complexExpression.evaluate()); //true

It can be a lot to wrap your head around, but the beauty of the composite pattern is how it creates an elegant way to simplify representing very complex logic. This sets the stage for our rules engine, and next time we’ll cover how we can use this pattern to help us parse logical statements.